How to simulate
everything (all at once) The Universal Turing Machine (or UTM) is well known. It is a Turing machine that takes as input a binary representation of a Turing machine and a binary representation of some arbitrary input and simulates the workings of the specified Turing machine on the specified input. In what follows we'll assume three tape Turing machines (input, work, output), with a binary alphabet, where 0 corresponds to an unmarked square and 1 is marked. Input to the Turing machine is assumed to be finite (i.e. there are only finitely many 1s on the tape). While I speak of a single input, it could easily encode finitely many individual binary strings into the single binary string. Less well known is what I call the Complete Turing Machine. It simulates in parallel all Turing machines on all input. There is a small trick to this, but it is not difficult. Since Turing machines can go on forever, we can't wait for one to finish before simulating the next, but have to simulate them in parallel. It is easy enough to simulate two Turing machines in parallel, performing a step from the first then a step from the second and so forth: step 1 of machine 1, step 1 of machine
2, This approach can only interleave finitely many infinite sequences, but we require infinitely many Turing machines. Thankfully, there is a well known trick to interleave infinitely many infinite sequences into a single infinite sequence. For example: step 1 of machine 1, In this way, every Turing machine gets to execute every step (if a Turing machine halts we just skip over each remaining step allocated to it). We could specify a first draft of the Complete Turing Machine in C-like pseudocode: for (i = 0; ; i++) tm[] is an (extendable) array of representations of configurations of Turing machines including information about their transition tables, their current tape, their current state, and the location of the tape head. It starts uninitialised. initialise_tm(tm, i) is a function that initialises a Turing machine representation to start in the starting state, with a blank tape, the tape head at the start position, and using the ith transition table (on some recursive coding of all legal transition tables). compute_next_step(tm) is a function that takes such a representation and simulates a single computational step on it. It is a standard core part of a Universal Turing machine. This will simulate all Turing machines (including non-terminating ones) running on a blank input tape. We actually want all Turing machines on all inputs, but we can achieve this by a small modification to the initialisation function. Instead of using i as a code for a transition table, it now treats i as coding a pair of natural numbers (x, y) (on some recursive coding of all pairs of naturals) then initialises the Turing machine to use the xth transition table and sets the input tape to the yth input tape (on some recursive coding of all finitely marked input tapes). Since the coding guarantees that all (x,y) pairs will be in this list (possibly using an ordering like the triangular one above), each transition table, input pair will be initialised at some point and every step of their computations will be run. So far so good. We now have a machine that will simulate all Turing machines on all finite inputs. The existence of such a Turing machine is known, but not all that well known. This is a shame, because it is a pretty amazing thing: in some ways much more amazing than the Universal Turing machine. Firstly, it computes all Turing computable functions (and evaluates them on all inputs). Obviously it also semi-computes all Turing semi-computable partial functions (it evaluates them on all inputs where there is a defined answer). However, thinking of what it does in terms of functions misses most of the glory of this machine. Consider sorting a finite list of natural numbers. This is a Turing computable function, but can be done in many ways. There is quick sort, merge sort, insertion sort, selection sort, bubble sort, and all their friends. The CTM doesn't just sort lists, it sorts them using each and every one of these distinct algorithms. It even sorts them with every subtle variation on each of these algorithms. At the first level of simulation, the CTM simulates all and only Turing machines. What about programs in C? Or functional and logical languages such as Haskell and Prolog? Or unusual models of computation like neural nets. We might think that there are algorithms that can be expressed in these types of languages which can't be expressed on a Turing machine and we'd like to simulate these too. Well, for each of these there is a Turing machine that acts as an interpreter for that language, and there is also a Turing machine that uses such an interpreter to run all programs in that language on all inputs (analogous to the CTM itself). So the CTM simulates a Turing machine which simulates all Haskell programs and another which simulates all Prolog programs and another which simulates all neural networks etc. The CTM's calculation thus includes simulations of all programs in all Turing complete languages and sub-Turing languages (most of which are yet to be invented) which are run on all inputs, but they are nested one level down — simulations inside simulations. The CTM also simulates physical phenomena.
If our universe is Turing computable, then it will be simulated
by this CTM. Indeed since there are infinitely many Turing machines
that express the same algorithm, it will be simulated infinitely
many times in parallel. The CTM will also simulate it with every
possible recursive set of initial conditions. In between these threads
will be simulations of the hailstone numbers, chess, tropical cyclones,
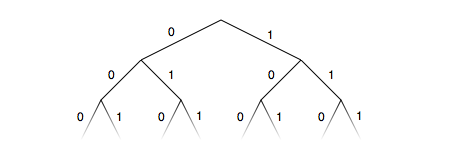
the game of life, lolcats, and this entire simulation itself. Adding oracular computation What can't a CTM simulate? I'm sure many readers will immediately think of their favourite uncomputable function or process. Others will think of counting arguments: there are only a countable infinity of Turing machines and there are an uncountable infinity of processes, so almost all of them must be impossible to simulate. For example, consider an endless simulation of an empty room with a light bulb that flashes on and off: for each one minute block of time, the light stays on or stays off, but at the end of each minute it may or may not change to the other state. There are uncountably many such sequences of flashes, as they correspond directly to the infinite bitstrings (e.g. a string where the nth bit is 1 if and only if the light is on during the nth minute). There are thus uncountably many lightbulb simulations, and so not enough Turing machines to be able to simulate all of them. Similarly, there is a lightbulb simulation whose pattern of flashes spells out a lookup table for the halting problem and we're going to have a lot of trouble simulating that one. This is a compelling argument. Surprisingly it is wrong. It turns out that we can simulate all such sequences of flashing lights so long as we do them simultaneously. Let's start with two parallel simulations: one with the light off for the first minute and one with it on. We then fork each of these simulations, simulating both ways the next minute could go. We continue in this way, forking all the existing simulations at each stage and having an exponentially increasing number of simulations in parallel. We are building up an infinite binary tree of simulations in a breadth first manner.
Infinite binary trees are remarkable for having an uncountable infinity of branches (each of which is infinitely long) coming down from the root, but are comprised of only a countable infinity of vertices and edges. This is a pretty surprising feature, and is only possible because the branches overlap so much with each other (each branch overlaps with an uncountable infinity of other ones). Because of this strange fact, this tree structure allows us to simulate the seemingly unsimulable. The individual edges on the tree correspond to the simulated minutes of time. The fact that they are countable allows our parallel simulation to get through all of them. The branches correspond to the entire infinite sequences of light flashes. For each of these branches (an uncountable infinity) every stage of that branch gets simulated at a particular point in the computation. Each branch is simulated in temporal order and the stages depend appropriately on the stages before. For example, if the heat of the glass bulb is modelled, its level will depend upon the exact sequence of flashes that lead up to that moment and this will be modelled perfectly. In other words, this elaborate branching computation will faithfully simulate each of these uncountable infinity of sequences in parallel. How exactly could this process be made precise? Let's represent each simulation by an oracle machine. This is a Turing machine with an additional read-only tape that is called an oracle tape. The state transition table is allowed to refer to what is under the tape head on the oracle tape as well as what is under the tape head on the input tape or the work tape. There is nothing mysterious so far. What is normally mysterious about oracle machines is that we usually consider that this oracle tape begins with infinitely much input on it. If the oracle tape begins with an infinitely long bitstring on it, the oracle machine can potentially do all kinds of interesting things, such as solving the halting problem. However let's set such possibilities aside and consider it with an oracle tape that consists only of zeros. This won't allow it to compute anything a Turing machine can't compute, and there is a Turing machine that can simulate any such (blank-oracle) oracle machine. Indeed this simulating Turing machine is just a trivial modifiication of a Universal Turing machine. Consider an oracle machine that simulates a room with a light in it, and has this light be on during the nth simulated minute if and only if the nth square of the oracle tape is a 1. As the oracle tape starts with only 0s, it simulates a light that is always off. Now consider a Turing machine that simulates two such oracle machines in parallel, but before it simulates the nth timestep for each oracle machine, it alters the representation of the configuration of the second machine to put a 1 on the nth square on its tape. Since the simulated machine couldn't have looked at a square that far away yet, it will just behave as if it were given an infinite bitstring of 1s. In this case it will simulate a light that is always on. So the main Turing machine will be simulating a light that is always on and a light that is always off in parallel. Now lets add the infinite branching, with some more C-like pseudocode: initialise_om_with_room_simulation_program(om[0]) initialise_om_with_room_simulation_program(om) sets up the specified oracle machine with the transition table that will make it perform a simulation of the room with the flashing lightbulb (whose state in minute n will be determined by the nth square of its initially blank oracle tape). set_o_tape_square(om, i, value) just alters the ith square of the oracle tape of the oracle machine to be equal to the given value. fork(om1, om2) simply sets the entire configuration of the oracle machine om2 (its tapes, tape heads, current state, and transition table) to be the same as that of om1. These nested loops build up the infinite binary tree of computations in a breadth first manner. The outer loop counts the number of timesteps and the inner loops do the forking and the next step for each sequence. For each sequence of flashes, this program will simulate it: even a sequence that encodes a lookup table for the halting problem. There is no paradox here. There would be if a Turing machine could produce just one simulation that encoded a lookup table for the halting problem, but this one is produced along with everything else and can't be isolated, so it can't produce a paradox. This is related to the fact that while most of the individual sequences of bits have infinite Kolmogorov complexity, the set of all such sequences has very little Kolmogorov complexity. It is simpler than the sum of the complexities of its parts. Indeed for some of these parts, the whole is simpler than just that one part. This may seem odd, but is also true of, say, a sphere. It can be decomposed into interlocking parts of extreme complexity, but the whole is simpler than one of these parts, and the whole cannot in general be used to derive a particular part. So where does this get us? What can we simulate using this trick? While the particular branching simulation trick was used with a particular scenario in mind (a room with a lightbulb), it can be applied much more broadly than that. We can make the initialisation function initialise the starting oracle machine to have any transition table we like and any input we like. The pseudocode above can thus be used to do general purpose oracular computation. For example, if we set up the starting machine to treat its oracle tape as coding the halting problem, we could run a machine that uses this to calculate the busy beaver function, or Chaitin's Omega constant, or to implement the uncomputable AI algorithm, AIXI. Of course it will go wrong in all but one branch of the entire branching tree of simulations, but in that branch it will correctly use its halting problem oracle to compute another non-Turing-computable function. The branching trick is analogous to Borges's story about the Library of Babel, which contains all possible 410 page books of a certain format. This library contains many of the great historical works, but they bear no causal relation to the originals. They are merely there because everything is. Similarly, we have all infinite bitstrings, so are guaranteed to have all the most interesting ones. If this were all, it wouldn't be that interesting, but this library of infinite strings are not the end result. They feed into the oracle machines and can lead to infinite computations of exquisite complexity. We've seen that we can simulate any particular oracle machine with all oracle tapes simultaneously. But why hard code in a particular oracle machine? We could follow the UTM and have our branching computation take the oracle machine to run as an input. Or we follow the CTM and combine the branching trick of this section with the interleaving trick of the previous section.We can thus have a single Turing machine that simulates all oracle machines in parallel, running on all inputs, and with access to all oracle tapes. Since a Turing machine is equivalent to
an oracle machine with a blank oracle, this computation effectively
includes simulations of all Turing machines on all inputs too. However,
if you really want you could interleave this branching computation
with a regular CTM, explicitly simulating all Turing machines on
all inputs as well as all oracle machines with all oracle tapes
on all inputs. This even has the advantage that your addition of
all the oracle machines only slows down the Turing machine simulation
by a factor of two. Adding infinite inputs When I have said 'all inputs' so far in this piece, I have meant all finite inputs. But do we need to keep to this restriction? No. Let us return from oracle machines to Turing machines. The branching trick from the previous section can be used to allow us to simulate a particular Turing machine on all infinite inputs. We simply initialise the original Turing machine to have a blank input tape and then fork it at every timestep, with one copy having the next square of the input tape set to 1. This is exactly the same as the oracle machine version, but changing the input tape instead of the oracle tape. This will run that Turing machine on all infinite inputs in parallel. As before, all these tricks can be combined. The only difficulty is combining the two types of branching trick to allow oracle machines with infinite inputs. Instead of forking each simulation into two at each timestep (0 and 1), just fork it into four. Put 0 on both the nth square of the input tape and the nth square of the oracle tape on the first one, put 0 and 1 respectively for the second, 1 and 0 for the third, 1 and 1 for the fourth.This infinite quaternary tree does the job of both binary trees. Note that the infinite input trick also
generates all finite inputs, so we no longer need to have the complication
of running through all Turing machine, input pairs from the original
CTM specification. Bringing it all together We now have a single Turing machine that
simulates: We shall call this a Hyper-Complete Turing Machine, or HCTM. This is a very startling object! I think many people would be surprised that a Turing machine is powerful enough to simulate so many things. If our universe is Turing computable, then this simulates it. If our universe is not Turing computable, this might still simulate it — so long as there is some way to do so with access to an infinite amount of information. For example, it simulates universes which contain rods of arbitrary real valued lengths. It also simulates hypercomputational universes in which you can build accelerating Turing machines that do each step in half the time of the step before, allowing an infinite amount of computation in a finite time. It simulates universes in which there are physical devices that can (contra Gödel) decide the truth of any sentence in first order arithmetic. However there are things that require too
much information to be simulated. While it can store a countable
infinity of infinite precision real numbers, it cannot store an
uncountable infinity of them, so I don't see how it could faithfully
simulate all universes that contain an uncountable infinity of rods
with real valued lengths. If consciousness is created by a certain kind of computational process (even a non-Turing computable one), then it appears that it would produce conscious observers in some of its simulated universes. Indeed, it would produce infinitely many of them, having a great variety of experiences (perhaps all possible experiences). I don't know whether simulating all universes really would create consciousness, but lets at least see what would follow from that. David Deutsch has argued that there are
virtual reality environments that Turing machines cannot simulate
(by listing the environments each Turing machine simulates and diagonalising
out to have the nth minute of the impossible simulation
be different to the nth minute generated by the nth Turing
machine). This is true if we are only allowed to simulate a single
environment at once. However, if I were not a flesh and blood human
hooked up to a computer, but a computational process within a computer,
then the simulation could fork that process as well. For example,
take the simulated room with a flashing light and add a human being.
If that simulated human being were conscious, then when the computation
forks, a conscious being would behold the light being on and a conscious
being would behold the light being off. In the nth minute,
there would be 2n different conscious states
being simulated with memories of all the different sequences to
that point. If the conscious being were inside the simulation like
this, then (contra Deutsch) they could observe any environment made
up of individually simulable pieces. There could even be branches
of the computation with conscious observers who have access to programmable
hypercomputers, who can play with them to their heart's content. I have said a lot about the CTM and HCTM simulating computations and physical processes. One might object that they aren't really simulating things. For example, one might think that the CTM is only directly simulating Turing machines and that indirect simulation is not real simulation, so it is not simulating Haskell programs or physical environments. I'm not an expert in how to define simulation, but let me say that if this is correct, then the computer on your desk never simulates physical processes either, for there are similar levels of indirection there. For example, it might be simulating a java virtual machine, which is simulating a bouncing ball. But at least as we typically use the word, we say that the computer is simulating a bouncing ball. One might instead object that branching computations are not really simulating the contents of all the branches, since when a simulation is forked the newly made copy didn't really do the first part of the computation. I find this objection unpersuasive too, as routine simulations often require the forking of computational threads and we normally talk about these threads as if they really do share a common history. However, I'm prepared to accept that there
may be narrow senses of simulation in which some of the things that
go on in these grand computation aren't being 'simulated'. That
is fine, I'm just arguing that there is a broader sense of simulation
in which they are, and that this sense seems to closely match common
usage. What is the relevance of CTMs and HCTMs? I have to admit that I can't see any practical upshot. It is doubtful that we could run the computation. Firstly, the branching computation trick forces an exponential slowdown, making timely results unlikely. Even if this were considered acceptable, it would require the Turing machine to be able to safely operate for ever and to use an infinite amount of memory. Moreover, even if we could get around this, it would appear to have no use to the outside world. Internally, it would either generate no conscious experience, or it would generate a vast amount, presumably with as much suffering as bliss. If the CTM and HCTM have any use at all,
it is likely to be in theoretical developments in computer science,
physics, or philosophy. For example, they might bear on debates
about whether the universe is Turing computable, and whether the
fundamental layer of reality is a CTM or HCTM. These would be a
pretty plausible candidate, for while they are relatively simple
to specify, they would give rise to a vast amount of complexity
within some of their computational branches, and apparently enough
to fit all of our physical laws and initial conditions. Indeed Jürgen
Schmidthuber has explicitly suggested that the CTM might be
this ultimate layer, and Max
Tegmark has suggested that all the richness of mathematical
objects might be this ultimate layer. This HCTM lies somewhere in
between. As a final thought, consider that the HCTM is itself a Turing machine. It will thus be simulated somewhere within the standard CTM. While all the messing around with branching simulations has been useful for showing us just how much we can simulate (all at once!) we don't actually need to explicitly code it up. The CTM eventually finds an HCTM and thus already contains these simulations of oracle machines and infinite inputs. I mentioned before that while the only things a CTM directly simulates are Turing machines, some of these Turing machines simulate Neural Networks or Haskell programs, so the CTM indirectly simulates these too. Similarly, the CTM directly simulates an HCTM which then directly simulates preposterously many non-recursive things, so the CTM also (indirectly) simulates all of these too.
|