Degrees of Truth, Degrees of Falsity
Toby Ord


In this paper I recall the reasons in favour of extending the classical conception of truth to include degrees of truth as well as truth value gaps and gluts, then provide a sketch of a new system of logic that provides all of these simultaneously. Despite its power, the resulting system is quite simple, combining degrees of truth and degrees of falsity to provide a very flexible and elegant conception of truth value.


One way to extend classical logic is to add new truth values. In classical logic, we have but two: True and False. Sentences are thus either absolutely true or absolutely false.


Fuzzy Logic

People have argued that this dichotomy is not warranted. For example, consider sentences of the from, 'x is bald'. For some values of x (i.e. for some people), this sentence is clearly true. For others it is clearly false. However, there doesn't seem to be any precise line between being bald and not being bald. For some people it does not seem to be completely true to say that they are bald or to say that they are not bald. Depending on one's conception of baldness, this troublesome band might be thick or it might be quite thin, but it certainly seems to exist.

One way to understand this situation is to claim that there are degrees of truth. These are typically represented by the real numbers in the interval [0,1]. The extreme points (0 and 1) represent absolute falsity and absolute truth, while the values in between represent intermediate truth degrees. We can then say that the truth value of 'Michael is bald' is 1 (it is absolutely true), the truth value of 'John is bald' is 0 (it is absolutely false) and the truth value of 'Paul is bald' is 0.3. Or perhaps it is 0.4. We do not need to be able to say precisely, but merely to insist that there is some answer.

When a system of logic uses degrees of truth it is called fuzzy logic. Such systems typically define the logical operations as follows:
¬P
 = 1 - P
P ∨ Q
 = max(P, Q)
P ∧ Q
 = min(P, Q)

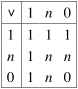
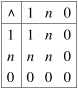
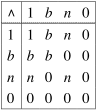
Such systems thus allow us to assess sentences involving one or more vague properties, such as warm, old, strong, fit, happy, bright and so forth. This is potentially of considerable philosophical use in tackling vagueness and the related sorites paradox (although it is by no means a panacea).

Fuzzy logic also has more practical uses, having made a considerable impact in engineering within the domain of control systems. It is often convenient to program a series of logical conditions and corresponding actions into a machine, and fuzzy logic allows the values of the propositions involved to come directly from the machine's sensors (such as thermometers or motion detectors). Fuzzy logic can then allow the machine's effectors (such as the temperature of the machine's heating element) to vary continuously as its inputs change, avoiding the discrete jumps that would occur using classical logic. Of course such behaviour could be directly programmed into the machines, but allowing the behaviour to be governed by a system of logic has additional benefits such as ease of design and the potential to prove results about its operation.


Truth Value Gaps

The restrictiveness of the truth values in classical logic is also challenged on another front. Suppose that you have a radioactive atom and want to know the truth value of the sentence 'The atom will decay within the next half-life'. On the most common interpretation of quantum mechanics, this sentence does not seem to have a determinate truth value before the experiment is performed: it would appear to be neither true nor false. This state is sometimes referred to as a truth value gap. One might even think that this occurs in less exotic statements about the future such as 'It will rain in Melbourne on the first day of Autumn in 2077'.

Furthermore, one might think that sentences which suffer reference failure are neither true nor false. For example, 'The greatest prime number is not even' or 'Sherlock Holmes is wise'. The same might be said about sentences that suffer from category mistakes, such as 'The capital of Ireland is 3', or that are ungrammatical, such as 'Runs capital violet the.' These sentences make different kinds of mistakes and the best way to understand some of these might be to say that the sentences are meaningless, or otherwise flawed, in such a way as to prevent them from being true or false.

Alternatively, if you subscribe to an understanding of truth which equates it with verifiability, then you might also run into truth value gaps. This would occur when there is a sentence P such that neither P nor ¬P can be verified.

None of these arguments are definitive, but there is at least a case for introducing a new truth value for sentences that are neither true nor false. Let us use the symbol 'n' for this truth value and continue to use '1' and '0' for True and False respectively. We could then use the following tables to define how the familiar logical connectives operate on these values:

These tables seem to capture the relationships involved and thus allow us to form and evaluate complex sentences built up of statements that may be neither true nor false.


Truth Value Gluts

There is also another, quite different, reason for being attracted to three valued logics. Consider the familiar troublesome sentence: 'This sentence is false'. If it is true, then by virtue of its meaning, it must be false. If it is false, then since it claims this very fact, it must be true. In either case, it would appear to be both true and false. We might then be tempted to have a new truth value to represent being both true and false. We could denote it by 'b' for 'both'.

One objection to this is that it is a mistake to assume that the liar sentence must be true or false — perhaps it is neither. This would lead us once again to truth value gaps. Alternatively, we might think that there is some other form of mistake here which is not immediately analysable, but which will be solved at some point in the future. This is quite plausible and thus philosophers need not be committed to truth value gaps or gluts.

Perhaps surprisingly, the truth tables for three valued logic using b turn out to be exactly the same as those using n. However, the difference between the two logical systems comes in the way that proofs are deemed acceptable. Classically, we think that the hallmark of logical validity is truth preservation: for an argument to be valid, it must be impossible for its premises to be true without the conclusion also being true. There are two obvious ways to generalise this notion to three valued logics and these correspond to whether or not we think of the third value as being true.

Thus, if our third value is n, the appropriate constraint on truth preservation is that valid arguments cannot start with premises valued 1 and deliver a conclusion valued 0 or n — valid arguments cannot take us from something with truth to something without. On the other hand, if the third value is b then it possesses truth so, the truth preservation constraint dictates that valid arguments cannot start with premises valued 1 or b and deliver a conclusion valued 0.

In the first case, n acts much like 0 and in the second case, b acts much like 1. We say that in the first case 1 is designated while n and 0 are not. In the second case 1 and b are both designated while 0 is not. Being designated corresponds to having the truth that we want to preserve in logical implication. Thus we can say that valid arguments can never take us from designated premises to non-designated conclusions.

Another, particularly important difference stems from the role of contradictions in these logics. In classical logic, it is well known that contradictory premises can entail any conclusion — a law known as ex falso quodlibet. This seems rather bizarre, but is typically brushed over on the grounds that we should never adopt contradictory premises in the first place. However, life is not always that easy, and sometimes contradictory premises sneak in unawares or are foisted upon us. For example, unbeknownst to its creators, the first formulation of calculus (which used infinitesimal quantities) was inconsistent. So too are the national laws that govern us. Even small sections of such laws typically contain many inconsistencies. For example, it can be shown in the British Immigration act that certain people both can and cannot become citizens.

Non-classical logics can deny the rule of ex falso quodlibet and those that do so are known as paraconsistent logics. An important example of such a logic is the three valued logic with b. This allows us to reason formally about such systems as the original infinitesimal calculus or the British Immigration act without being reduced to gibberish. Contradictory conclusions can be drawn, but they are limited to the the area in which the contradictions arose and the paraconsistent reasoning can therefore be more robust. Thus, even if one does not believe that statements can be both true and false, it may still be tempting to use a logic involving b for pragmatic reasons.


Generalised Theories
 
Given the reasons both for truth value gaps and gluts, one might wonder why we shouldn't allow both. Indeed there is a system of four valued logic known as FDE which allows sentences to be true, false, both or neither. We can then define the standard logical operations using the following diagram.

The negation of a value is the value found by reflection in the line between n and b. Thus 1 and 0 swap places, while n and b are unchanged by negation. The disjunction of two values is their least upper bound and the conjunction of two values is their greatest lower bound. Note that the partial ordering used here ranks values according to increasing truth and decreasing falsity. Thus disjunction can be said to maximise truth and minimise falsity, while conjunction minimises truth and maximises falsity. These definitions can be seen to agree with our intuition and can also be represented as truth tables:

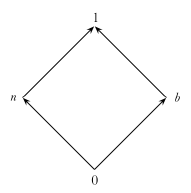
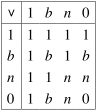
We can then define logical inference by saying that 1 and b are designated while n and 0 are not. Thus valid arguments are those that cannot take us from premises valued 1 or b to conclusions valued n or 0. This system has received considerable study and is a very natural generalisation of the two kinds of three valued logic.

But why stop here? Is there some way to join up the degrees of truth from fuzzy logic with the gaps and gluts? One way would be to take the values [0,1] from fuzzy logic and to identify 0.5 as n. By calculating the truth tables for fuzzy logic where propositions take the values 0, 0.5 and 1, we can see that the familiar truth tables for the three valued logic come out. It might thus seem that we have unified fuzzy logic and truth value gaps.

However, there are some problems with this approach. For one thing, consider that the truth tables for three valued logic with gluts are the same as those for three valued logic with gaps. It is just the rules of inference that change. Thus, the argument above should also imply that we can interpret 0.5 as b, but this is clearly leading us into trouble.

The problem is intimately related to the rules of inference for fuzzy logic, which we have not yet discussed. As mentioned previously, logical inference should preserve truth, but when truth comes in degrees, how much should it preserve? A very natural answer is to attach a real valued parameter, τ, to the notion of implication, where τ represents the required degree of truth. Thus for an inference to be valid, it must be impossible for the premises to all have a degree of truth of at least τ whilst the conclusion has a degree of truth below τ. In other words, values greater than or equal to τ are designated.

We can then say that an argument is valid simpliciter (i.e. without reference to a parameter) when it is valid for every value of τ. This is the same as saying that the argument can never lead to a conclusion that is less true than the weakest premiss.

Unfortunately, this conflicts with our understanding of n and b, because n can never be designated and b is always designated. Thus the identification of n with 0.5 works only for fixed values of τ greater than 0.5 and the identification of b with 0.5 works only for fixed values of τ less than or equal to 0.5.

Whilst this method might therefore have some limited success in joining one or the other of n and b to the degrees of truth from fuzzy logic, it is not altogether successful and could never allow both values simultaneously. Moreover, there would seem to be good philosophical reasons to think of each of them as distinct from 0.5, which in fuzzy logic denotes something akin to half true.


A New System

A more promising approach is to consider degrees of truth alongside degrees of falsity. Let each truth value be represented by a pair of real numbers from 0 to 1. We can thus represent truth values as points on the following diagram:



In a truth value (p, q), p is the degree of truth and q the degree of falsity. Thus the point at the top (1,0) represents absolute truth while the point at the bottom (0,1) represents absolute falsity. The point on the left (0,0) represents the most extreme absence of truth and falsity, whilst the point on the right (1,1) represents the most extreme excess of truth and falsity. Note also the similarity of this diagram and the one used earlier for four valued logic:


This new space of truth values provides us with a great degree of flexibility. For example, consider the following regions:

Over-defined (truth value glut).
Under-defined (truth value gap).
Well-defined.

These are the values used in fuzzy logic.
More true than false.
More false than true.
Equally true and false.
More than half true.
More than half false.

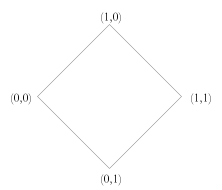
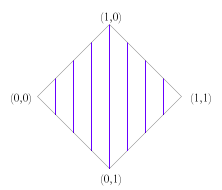
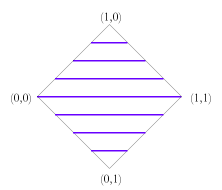
As can be seen, this set of truth values takes us beyond those present in fuzzy logic and four valued logic, but the extension is very natural.

The definitions of the logical operations also come very naturally, combining the methods of fuzzy and four valued logics.
¬(p, q) = (q, p)

Thus negation reverses the degrees of truth and falsity.

Note that negation is simply a vertical reflection in the lattice.
 (p1, q1) ∨ (p2, q2) = (max(p1, p2), min(q1, q2))

 (p1, q1) ∧ (p2, q2) = (min(p1, p2), max(q1, q2))

Thus disjunction maximises truth and minimises falsity, while conjunction does the reverse.

Note that disjunction is simply the least upper bound and conjunction the greatest lower bound.

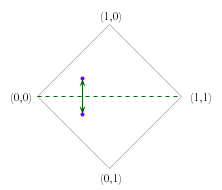
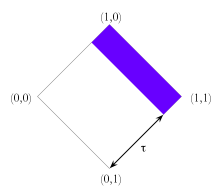
Note that when restricted to classical values, these connectives give the classical results; when restricted to 0, n, b, 1 they give the four valued logic results; and when restricted to the well-defined values, they give the fuzzy logic results.

As with fuzzy logic, we can designate those values where the degree of truth is greater than or equal to the value of a parameter, τ. As with the three and four valued logics, n is never designated while b is always designated. Other under-defined or over-defined values may also be designated, depending on their degree of truth. As per the three and four valued logics, the falsity of the value is irrelevant when it comes to considering designation — only the degree of truth matters. We can again define validity simpliciter as validity for all values of τ.
The designated values.

Setting τ to equal 1 gives a particularly natural logic.

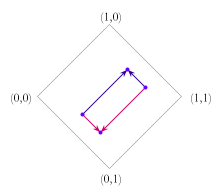
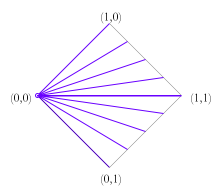
On reflection, we can see a variety of potentially important properties of these new truth values, such as definedness, net truth and proportional truth:
Lines of equal definedness.

   where the definedness of (p, q) = p + q

This takes values from 0 to 2, with 1 representing 'well-defined'.
Lines of equal net truth.

   where the net truth of (p, q) = p - q

This takes values from -1 to +1.
Lines of equal proportional truth.

   where the proportional truth of (p, q) = p / q

This takes values from zero to infinity and is undefined when the truth value is (0, 0).

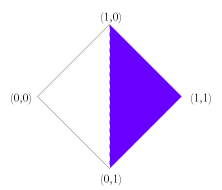
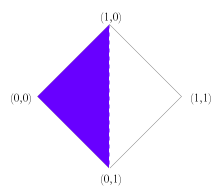
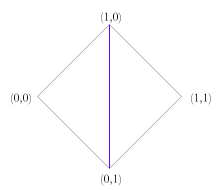
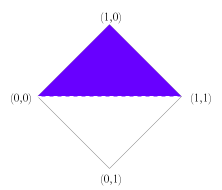
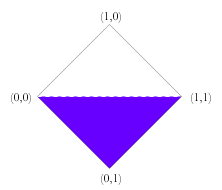
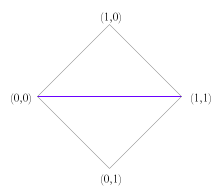
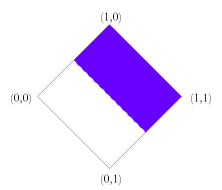
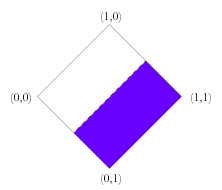
Note that there are also subsets of this space of truth values which are of considerable independent interest, and for which the rules above can be easily adapted. For example, there is the triangle formed by removing the over-defined values. This leads to a natural unification of the truth value gap based three valued logics with fuzzy logic. There is also the corresponding triangle formed by removing the under-defined values which leads to a unification of fuzzy logic with the truth value glut based three valued logics.

One could also consider the union of the well-defined values (those of fuzzy logic) with the points (0,0) and (1,1). This would give a minimal unification of four valued logic with fuzzy logic. In this case the conjunction and disjunction rules would have to be modified so to take account of the missing intermediate values. It is not obvious how best to do this.

Just as there are versions of fuzzy logic which have finitely many truth values between 0 and 1, so we could do this in the present system. One merely needs to posit a matching degree of falsity for every degree of truth. Similarly, we could restrict degrees of truth and falsity to rational values. Obviously these modifications could be combined with the ones above.


Further Work

This paper is just a bare sketch of a theory of degrees of truth and degrees of falsity, and there is much more work that could be done on the topic.

For one thing, it is worth noting that I have brushed over the use of conditionals in logics with more than two truth values. There are two standard ways to construct the conditional in three valued logics and at least two ways for fuzzy logic. I have not spent much time considering the natural ways to do so in the unified system as I have little intuition on the matter. Presumably there are at least two natural ways to do this, which would each form their own logic. Developing these would no doubt be an interesting project.

Similarly, I have not constructed a proof system and thus have no soundness or completeness results. I don't imagine that this would be too difficult and encourage others to do so.

Finally, and perhaps most importantly, I have not provided any example domains where such truth values would naturally arise. I feel that there are probably examples both philosophical and practical, but have no 'killer applications'. On the practical side, there may be applications where rules conflict (tempting us to move to a paraconsistent logic to avoid the calamitous ex falso quodlibet) and where these rules involve vague properties. I can envisage such fuzzy conflicts occurring both in legal systems and in engineering control situations. On the philosophical side, there may well be paradoxes which combine vagueness and self reference, where the ability to provide independent degrees of truth and falsity provides a way out. Whilst this space of truth values is clearly of independent interest, it could certainly benefit from some highly motivating examples.


References

Graham Priest, An Introduction to Non-Classical Logic, (Cambridge: CUP), 2001.




Note: — Since the writing of this piece I have become aware of a book which seems to include a theory of degrees of truth and falsity that is not unlike my own. I have not been able to examine this book, but from what I can tell, its truth values only include those whose definedness is less than or equal to 1. If so, it is a theory that unifies fuzzy truth with truth-value gaps, but does not address truth values which are over-defined. This book is:

Atanassov K., Intuitionistic Fuzzy Sets, (Heidelburg: Springer-Verlag), 1999.
 







    If you require a copy of this paper for your records, it is also available in a pdf version.